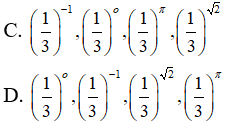Thông tin
Tin nổi bật
- LÃNH ĐẠO NHÀ TRƯỜNG CHÚC MỪNG BỘ MÔN THỂ DỤC THỂ THAO VÀ THÔNG TIN -THƯ VIỆN NHÂN NGÀY THỂ ...
- GIAO LƯU THỂ THAO CHÀO MỪNG 79 NĂM NGÀY THỂ THAO VIỆT NAM (27/03/1946 - 27/03/2025)
- NGÀNH QUẢN LÝ THỂ DỤC THỂ THAO - CƠ HỘI CHO NHỮNG NGƯỜI ĐAM MÊ THỂ THAO CHUYÊN NGHIỆP
- ĐẠI HỘI CHI BỘ KHOA KHOA HỌC CƠ BẢN NHIỆM KỲ 2025-2027
- HỘI NGHỊ CÁN BỘ VIÊN CHỨC NGƯỜI LAO ĐỘNG KHOA KHOA HỌC CƠ BẢN – TRƯỜNG ĐẠI HỌC KHOA ...
- ĐẠI HỌC LÀ GÌ, NHỮNG LÝ DO BẠN NÊN HỌC ĐẠI HỌC?
- Hoàng Thị Huyền Sinh viên Ngành Quản lý Thể dục thể thao - Khoa Khoa học Cơ bản xuất sắc ...
- ĐẠI HỘI CÔNG ĐOÀN KHOA KHOA HỌC CƠ BẢN NHIỆM KỲ 2023-2028
- KHOA KHOA HỌC CƠ BẢN THAM DỰ HỘI THAO NGƯỜI GIÁO VIÊN NHÂN DÂN TOÀN QUỐC NĂM 2022
- SÔI NỔI GIẢI BÓNG CHUYỀN HƠI GIẢNG VIÊN, SINH VIÊN CHÀO MỪNG KỶ NIỆM 90 NĂM NGÀY THÀNH LẬP ...
- GIẢI BÓNG BÀN KHOA KHOA HỌC CƠ BẢN MỞ RỘNG LẦN THỨ V - 2020
- Cán bộ, sinh viên Khoa KHCB Trường Đại học Khoa học tham gia chương trình nghệ thuật quần ...
- Bản tin chuyên đề của Đài PT-TH Thái Nguyên về Hội thi
- Đ/C PHẠM THỊ BÍCH THẢO BẢO VỆ THÀNH CÔNG LUẬN VĂN THẠC SỸ GIÁO DỤC HỌC
- Bộ môn lý luận chính trị - báo cáo seminar khoa học
Câu 1:Viết các số

theo thứ tự tăng dần

Câu 2:Tìm đạo hàm của hàm số y = log5(xex)

Câu 3:Tìm các khoảng đồng biến của hàm số y = x2e-4x

Câu 4:Tìm các khoảng nghịch biến của hàm số y = 3ln(x +1) + x – x2/2
A.(-1; 2)C. (-2 ;-1) và (2; +∞)
B. (2; +∞)D. (-∞; -2) và (-1 ;2)
Câu 5:Cho hai số thực a và b , với 0 < a < b < 1. Khẳng định nào sau đây là đúng ?
A. logba < 1 < logabC. logab < 1 < logba
B. logba < logab < 1 D. 1 < logab < logba
Hướng dẫn giải và Đáp án
| 1-A | 2-D | 3-C | 4-B | 5-C |
Câu 1:
Ta có -1 < 0 < √2 < π và 0 < 1/3 < 1 nên

Chọn đáp án A.
Câu 2:
Để thuận tiện, ta viết lại

Chọn đáp án D
Câu 3:
Tập xác định R.
Ta có:
y’ = 2xe-4x+ x2e-4x(-4) = 2e-4xx(1 – 2x)
Bảng biến thiên

Khoảng đồng biến của hàm số là (0; 1/2) .
Chọn đáp án C
Câu 4:
Tập xác định : (-1; +∞)

Bảng biến thiên :

Từ đó, khoảng nghịch biến của hàm số là(2; +∞) .
Chọn đáp án B
Câu 5:
Đặt c = b – a ta có c > 0. Do các hàm số y = logax và logbx nghịch biến trên (0; +∞) nên ta có logab = loga(a + c) < logaa = 1 và logba = logb(b – c) > logbb = 1.
Vậy logab < a < logba
Chọn đáp án C.
- KHOA KHOA HỌC CƠ BẢN – TRƯỜNG ĐẠI HỌC KHOA HỌC – ĐẠI HỌC THÁI NGUYÊN SẴN SÀNG CHÀO ĐÓN TÂN SINH VIÊN NĂM HỌC 2025-2026 [ 27/06/2025 07:39 ]
- TUYỂN SINH NGÀNH THÔNG TIN THƯ VIỆN TRƯỜNG ĐẠI HỌC KHOA HỌC NĂM 2025 [ 19/06/2025 00:00 ]
- Trường Đại học Khoa học công bố 5 chương trình đào tạo mới [ 10/06/2025 00:00 ]
- Tuyển sinh ngành Quản lý Thể dục Thể thao - Trường Đại học Khoa học năm 2025 [ 19/05/2025 00:00 ]
- Triển lãm tư liệu: “Vinh quang Đảng Cộng sản Việt Nam” [ 23/07/2020 00:00 ]
- Chương 2 – Lý thuyết Bài 4: Hàm số mũ và hàm số lôgarit [ 24/07/2018 00:00 ]
- Sơ đồ hóa 8 bài văn học trung đại lớp 11 dễ xuất hiện trong đề thi THPT môn Văn [ 24/07/2018 00:00 ]
- 50 câu trắc nghiệm từ vựng, ngữ pháp tiếng Anh hay có đáp án [ 23/07/2018 17:46 ]
- 150 câu trắc nghiệm chọn câu đồng nghĩa tiếng Anh (P1) [ 23/07/2018 17:42 ]
- 15 bài đọc hiểu tiếng Anh giải chi tiết – Tài liệu chinh phục đọc hiểu lovebook [ 23/07/2018 17:39 ]
- Cụm động từ (PHRASAL VERBS) thông dụng cần học cho thi THPT Quốc Gia [ 23/07/2018 17:36 ]
- 100 câu bài tập tiếng Anh dạng viết lại câu cực hay có đáp án [ 23/07/2018 17:31 ]
- 32 bài tập tìm lỗi sai tiếng Anh đáp án chi tiết [ 23/07/2018 17:27 ]
- 91 BÀI TẬP TÌM LỖI SAI THƯỜNG XUẤT HIỆN TRONG ĐỀ THI TIẾNG ANH [ 23/07/2018 17:08 ]
- 91 BÀI TẬP TÌM LỖI SAI THƯỜNG XUẤT HIỆN TRONG ĐỀ THI TIẾNG ANH [ 23/07/2018 17:05 ]
Văn bản mới
- THÔNG BÁO VỀ HỘI THẢO NGHIÊN CỨU KHOA HỌC ĐỔI MỚI PHƯƠNG PHÁP GIẢNG DẠY CÁC MÔN LÝ LUẬN ...
- Quyết định về việc công nhận thí sinh trúng tuyển hệ liên thông từ trung cấp lên đại học ...
- Tuyển sinh liên thông từ TC lên ĐH ngành Khoa học Thư viện.
- Quyết định về việc công nhận thí sinh trúng tuyển hệ liên thông từ TC lên ĐH hình thức VLVH ...
- Quyết định về việc miễn học phí cho sinh viên Nguyễn Thị Lan lớp Khoa học Thư viện hệ VLVH ...
- Đăng ký học cùng lúc hai chương trình
- Tuyển sinh liên thông từ TC lên ĐH nghành Khoa học Thư viện.
- Tuyển sinh ngành Khoa học Thư viện.
- Quyết định về việc công nhận sinh viên tốt nghiệp ĐH hệ liên thông từ TC lên ĐH hình thức ...
- Ấn định tên đề tài và giảng viên hướng dẫn đề tài sinh viên nghiên cứu khoa học năm ...
- Tuyển sinh lớp bồi dưỡng nghiệp vụ về khoa học Thư viện (Chương trình Thư viện - Thiết bị ...
- Tuyển sinh liên thông từ TC lên ĐH ngành Khoa học Thư viện.
- danh sách lớp học phần K13
- V/v tổ chức Hội nghị CB,VC năm học 2015-2016.
- Tập huấn công tác Phòng cháy chữa cháy trong nhà trường
Liên kết website
Thống kê website
Lượt truy câp: 3757896
Trong ngày:
Đang online: 20