Bài 1 (trang 23-24 SGK Giải tích 12):Tính giá trị lớn nhất và nhỏ nhất của hàm số:

a) y = x3– 3x2– 9x + 35 trên các đoạn [-4; 4] và [0; 5]

b) y= x4– 3x2+ 2 trên các đoạn [0; 3] và [2; 5]

Lời giải:

a)TXĐ: D = R.

y’ = 3x2– 6x – 9; y’ = 0 => x = –1 hoặc x = 3.

– Xét hàm số trên đoạn [-4; 4]

Vì -1 và 3 đều thuộc đoạn [-4; 4] nên ta tính các giá trị của hàm tại các điểm -4; 4; -1; 3.

Ta có: y(-4) = -41; y(4)= 15; y(-1) = 40; y(3)= 8

Vậy, giá trị lớn nhất của hàm số trên [-4; 4] là:

Giá trị nhỏ nhất của hàm số trên [-4; 4] là:

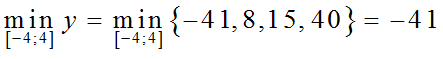
– Trên đoạn [0; 5]: ta thấy y’ = 0 tại x = 3 ∈ [0; 5]

Ta có: y(0) = 35; y(5)= 40; y(3)= 8

Vậy, giá trị nhỏ nhất của hàm số trên [0; 5] là:

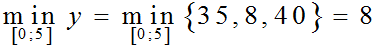
Giá trị lớn nhất của hàm số trên [0; 5] là:

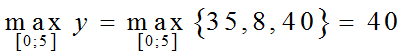
(Các phần b, c, d) dưới đây trình bày theo một cách khác, ngắn gọn hơn, nhưng vẫn bám sát theo cấu trúc trên.

b)TXĐ: D = R

y’ = 4x3– 6x

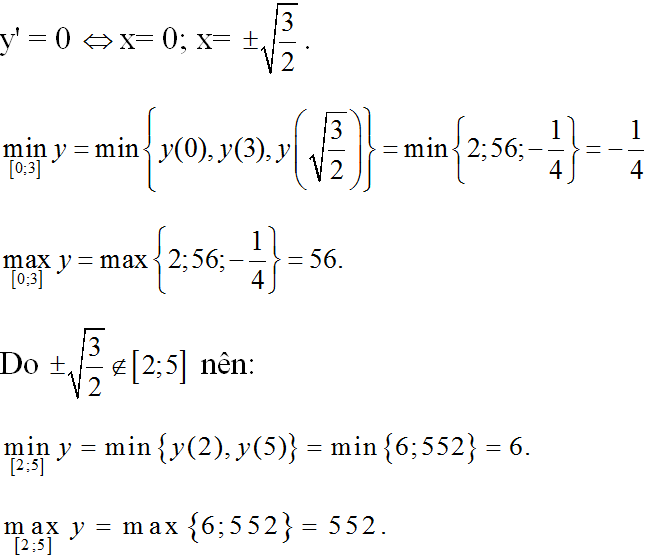
c)TXĐ: D = (-∞; 1) ∪ (1; +∞)

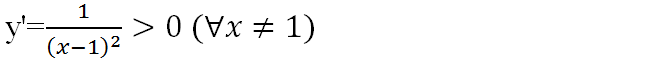
=> Hàm số đồng biến trên D.

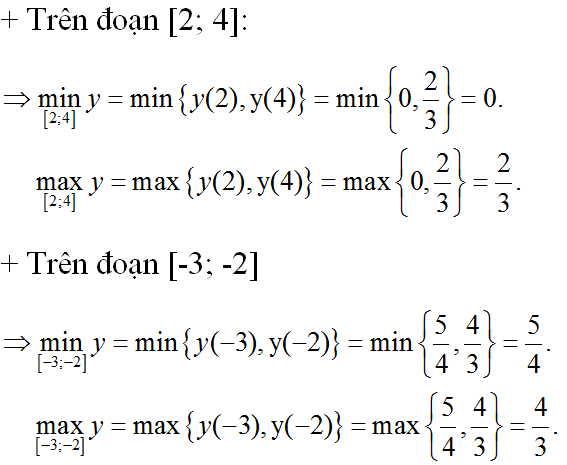
d)TXĐ: D = (-∞; 5/4]

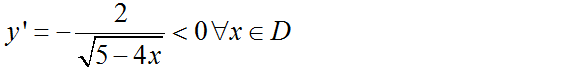
=> Hàm số nghịch biến trên D.

Khi đó trên đoạn [-1; 1]:

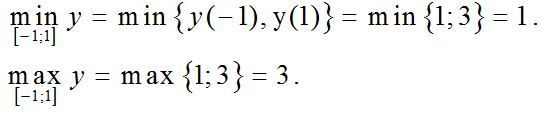
Bài 2 (trang 24 SGK Giải tích 12):Trong số các hình chữ nhật có cùng chu vi 16cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Lời giải:

Nửa chu vi hình chữ nhật là: 16:2 = 8cm

Gọi chiều dài hình chữ nhật là x (cm) thì cạnh kia có độ dài là (8 – x) (cm) (với x ∈ [0; 8]).

Diện tích của hình chữ nhật là:

y = S(x) = x(8 – x) = -x2+ 8x

Xét hàm số trên ta có: D = [0; 8]

y’= -2x + 8 = -2(x – 4)

y’ = 0 => x = 4

Hàm số đạt giá trị cực đại tại x = 4 (=> cạnh còn lại là 8 – 4 = 4) hay trong số các hình chữ nhật có chu vi 16cm thì hình vuông có diện tích lớn nhất.

(Lưu ý:Thay vì xét max, min như trên, bạn cũng có thể sử dụng Bất đẳng thức Cô-si với hai số x và x – 8 để suy ra kết quả tương tự.)