
Thông tin
Tin nổi bật
- LÃNH ĐẠO NHÀ TRƯỜNG CHÚC MỪNG BỘ MÔN THỂ DỤC THỂ THAO VÀ THÔNG TIN -THƯ VIỆN NHÂN NGÀY THỂ ...
- GIAO LƯU THỂ THAO CHÀO MỪNG 79 NĂM NGÀY THỂ THAO VIỆT NAM (27/03/1946 - 27/03/2025)
- NGÀNH QUẢN LÝ THỂ DỤC THỂ THAO - CƠ HỘI CHO NHỮNG NGƯỜI ĐAM MÊ THỂ THAO CHUYÊN NGHIỆP
- ĐẠI HỘI CHI BỘ KHOA KHOA HỌC CƠ BẢN NHIỆM KỲ 2025-2027
- HỘI NGHỊ CÁN BỘ VIÊN CHỨC NGƯỜI LAO ĐỘNG KHOA KHOA HỌC CƠ BẢN – TRƯỜNG ĐẠI HỌC KHOA ...
- ĐẠI HỌC LÀ GÌ, NHỮNG LÝ DO BẠN NÊN HỌC ĐẠI HỌC?
- Hoàng Thị Huyền Sinh viên Ngành Quản lý Thể dục thể thao - Khoa Khoa học Cơ bản xuất sắc ...
- ĐẠI HỘI CÔNG ĐOÀN KHOA KHOA HỌC CƠ BẢN NHIỆM KỲ 2023-2028
- KHOA KHOA HỌC CƠ BẢN THAM DỰ HỘI THAO NGƯỜI GIÁO VIÊN NHÂN DÂN TOÀN QUỐC NĂM 2022
- SÔI NỔI GIẢI BÓNG CHUYỀN HƠI GIẢNG VIÊN, SINH VIÊN CHÀO MỪNG KỶ NIỆM 90 NĂM NGÀY THÀNH LẬP ...
- GIẢI BÓNG BÀN KHOA KHOA HỌC CƠ BẢN MỞ RỘNG LẦN THỨ V - 2020
- Cán bộ, sinh viên Khoa KHCB Trường Đại học Khoa học tham gia chương trình nghệ thuật quần ...
- Bản tin chuyên đề của Đài PT-TH Thái Nguyên về Hội thi
- Đ/C PHẠM THỊ BÍCH THẢO BẢO VỆ THÀNH CÔNG LUẬN VĂN THẠC SỸ GIÁO DỤC HỌC
- Bộ môn lý luận chính trị - báo cáo seminar khoa học
Bài 1 (trang 43 SGK Giải tích 12):Khảo sát sự biến thiên và vẽ đồ thị của các hàm số bậc ba sau:
a) y = 2 + 3x – x3; b) y = x3+ 4x2+ 4x
c) y = x3+ x2+ 9x ; d) y = -2x3+ 5
Lời giải:
a)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = 3 – 3x2
y’ = 0 => x = ±1
+ Giới hạn:
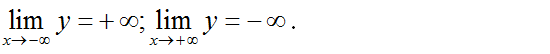
Bảng biến thiên
Hàm số đồng biến trên khoảng (1; 1 ).
Hàm số nghịch biến trên các khoảng (-∞; -1) và (1; +∞).
+ Cực trị:
Đồ thị hàm số có điểm cực tiểu là: ( 1; 0).
Đồ thị hàm số có điểm cực đại là: (1; 4).
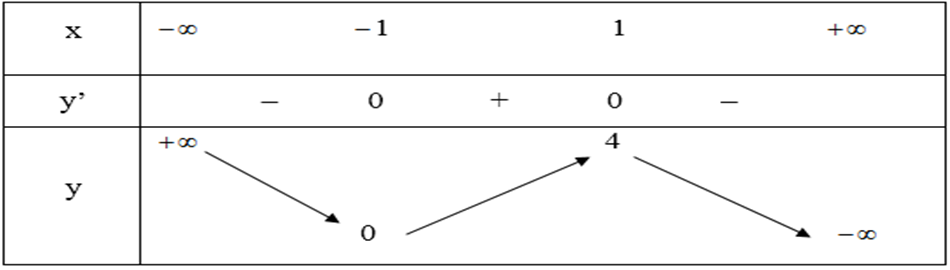
– Đồ thị:
Ta có x3+ 4x2+ 4x = 0 ⇒ x(x2+ 4x + 4) = 0
⇒ x(x + 2)2= 0 => x = 0; x = -2
+ Giao với Ox: (0; 0) và (-2; 0)
+ Giao với Oy: (0; 0) (vì y(0) = 0)
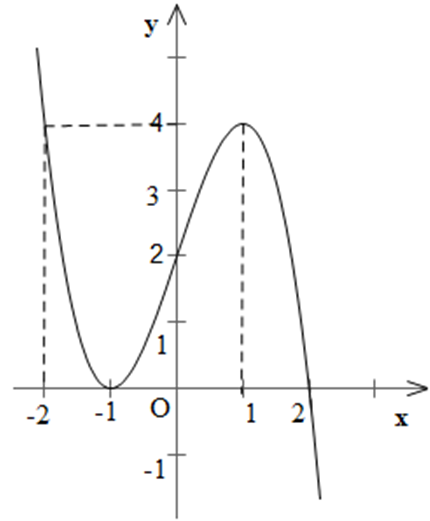
(Đồ thị hàm số nhận điểm (0; 2) làm tâm đối xứng.)
b)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = 3x2+ 8x + 4
y’ = 0 => x = -2 hoặc x = -2/3
+ Giới hạn:

Bảng biến thiên
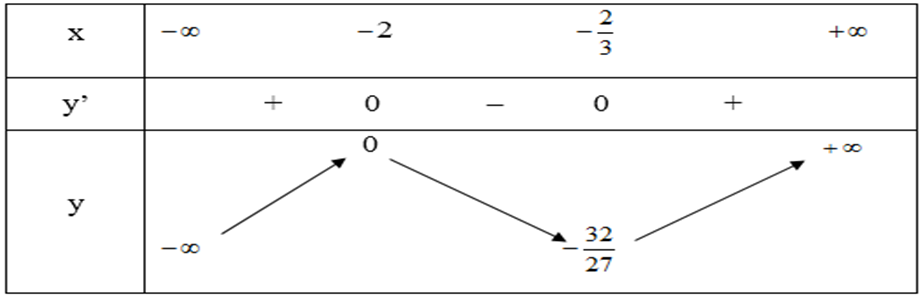

– Đồ thị:
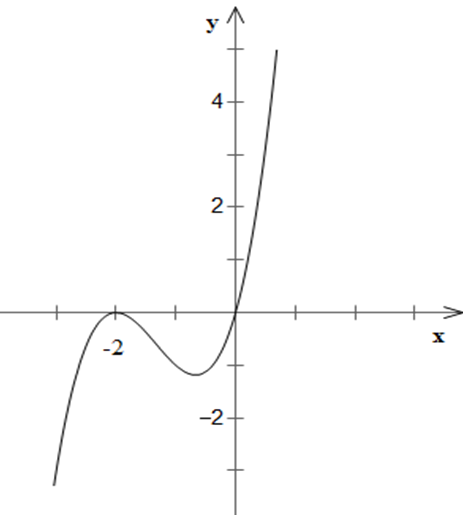
Ta có 2 + 3x – x3= 0 ⇒ x = -1 ; x = 2
+ Giao với Ox: (-1; 0) và (2; 0)
+ Giao với Oy: (0; 2) (vì y(0) = 2)
c)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = 3x2+ 2x + 9 > 0 ∀ x ∈ R
=> Hàm số luôn đồng biến trên R và không có điểm cực trị.
+ Giới hạn:
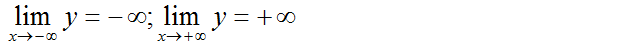
Bảng biến thiên
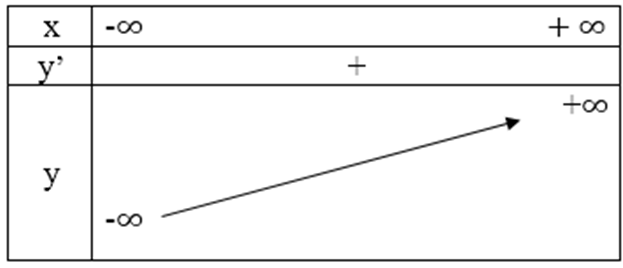
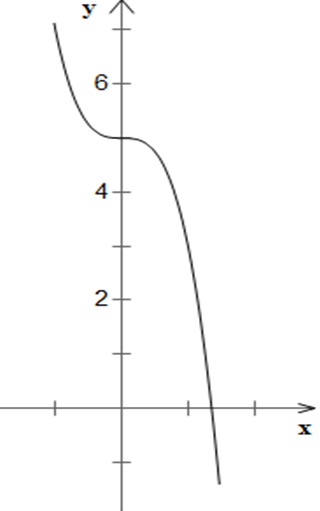
– Đồ thị:
| x | 0 | 1 | -1 |
| y | 0 | 11 | -9 |
d)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = -6x2≤ 0 ∀ x ∈ R
=> Hàm số luôn nghịch biến trên R và không có điểm cực trị.
+ Giới hạn:

Bảng biến thiên
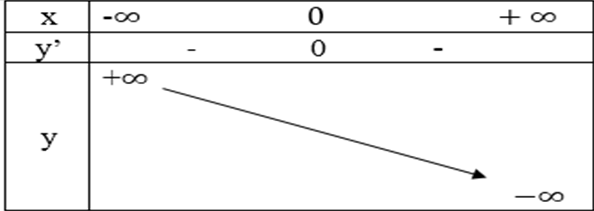
– Đồ thị:
| x | 0 | 1 | -1 |
| y | 5 | 3 | 7 |
Bài 2 (trang 43 SGK Giải tích 12):Khảo sát tự biến thiên và vẽ đồ thị của các hàm số bậc bốn sau:
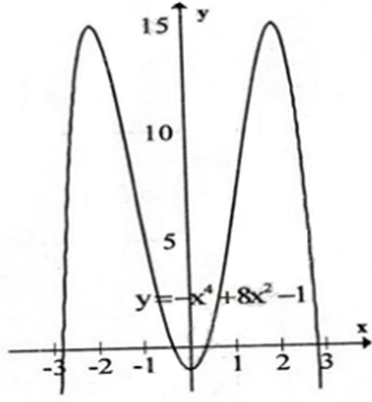
a) y = -x4+ 8x2– 1 ; b) y = x4– 2x2+ 2

Lời giải:
a)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = -4x3+ 16x = -4x(x2– 4)
y’ = 0 ⇔ -4x(x2– 4) = 0 => x = 0 ; x = ±2
+ Giới hạn:
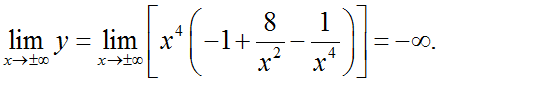
Bảng biến thiên
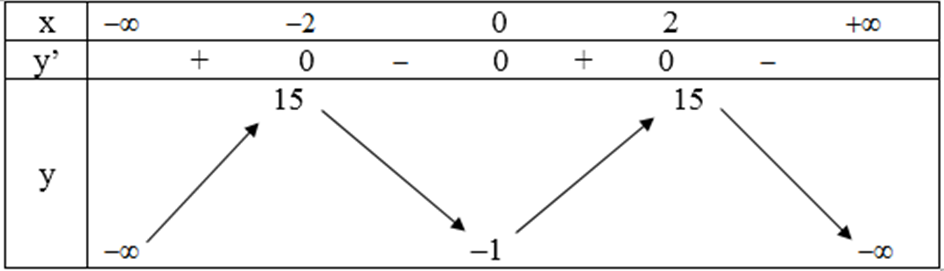
Hàm số đồng biến trên khoảng (-∞; -2) và (0; 2).
Hàm số nghịch biến trên các khoảng (-2; 0) và (2; +∞).
+ Cực trị:
Đồ thị hàm số có điểm cực tiểu là: (0; -1).
Đồ thị hàm số có hai điểm cực đại là: (-2; 15) và (2; 15).
– Đồ thị:
Hàm số đã cho là hàm số chẵn, vì:
y(-x) = -(-x)4+ 8(-x)2– 1 = -x4+ 8x2– 1 = y(x)
Do đó đồ thị nhận Oy làm trục đối xứng.
Ta có: -x4+ 8x2– 1 = 0 => x = ±√(4 + √15) ; x = ±√(4 – √15)
+ Giao với Ox: tại 4 điểm
+ Giao với Oy: (0; -1) (vì y(0) = -1)
b)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = 4x3– 4x = 4x(x2– 1)
y’ = 0 ⇔ 4x(x2– 1) = 0 => x = 0 ; x = ±1
+ Giới hạn:
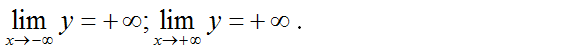
Bảng biến thiên
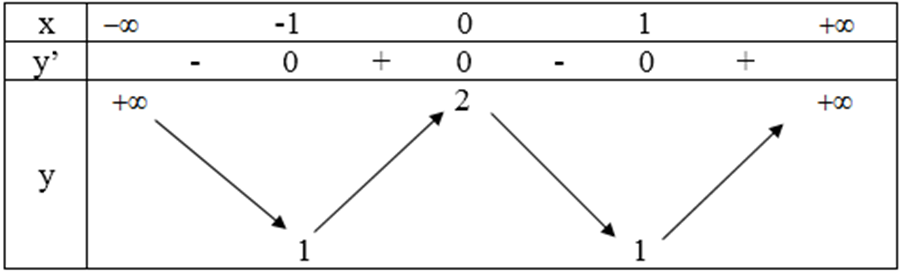
Hàm số đồng biến trên khoảng (-1; 0) và (1; +∞).
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1).
+ Cực trị:
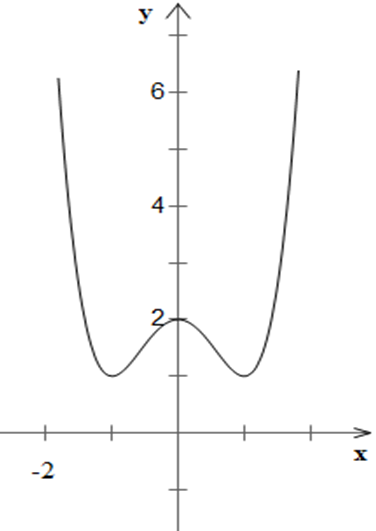
Đồ thị hàm số có hai điểm cực tiểu là: (-1; 1) và (1; 1).
Đồ thị hàm số có điểm cực đại là: (0; 2).
– Đồ thị:
Xác định tương tự như a) ta có đồ thị:
c)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = 2x3+ 2x = 2x(x2+ 1)
y’ = 0 ⇔ 2x(x2+ 1) = 0 => x = 0
+ Giới hạn:
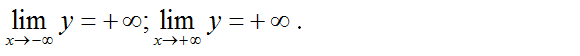
Bảng biến thiên
Hàm số đồng biến trên khoảng (0; +∞).
Hàm số nghịch biến trên các khoảng (-∞; 0).
+ Cực trị:
Đồ thị hàm số có điểm cực đại là: (0; -3/2).
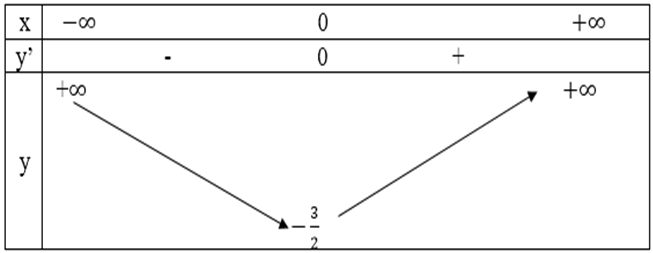
– Đồ thị:
Xác định tương tự như a) ta có đồ thị:
d)
– Tập xác định: D = R
– Sự biến thiên:
+ Chiều biến thiên: y’ = -4x – 4x3= -4x(1 + x2)
y’ = 0 ⇔ -4x(1 + x2) = 0 => x = 0
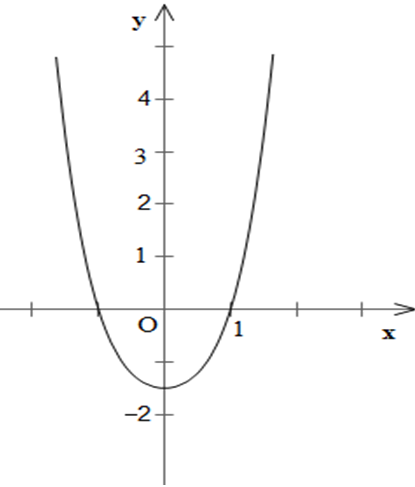
+ Giới hạn:
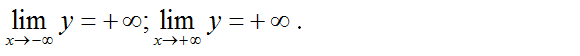
Bảng biến thiên
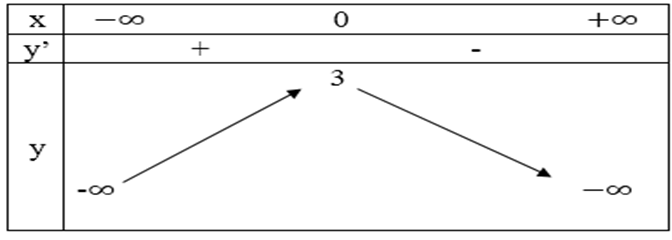
Hàm số đồng biến trên khoảng (-∞; 0).
Hàm số nghịch biến trên các khoảng (0; +∞).
+ Cực trị:
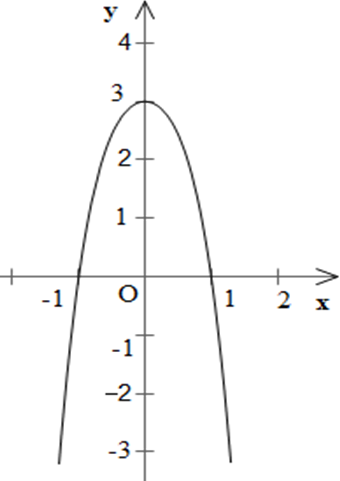
Đồ thị hàm số có điểm cực đại là: (0; 3).
– Đồ thị:
Xác định tương tự như a) ta có đồ thị:
- Triển lãm tư liệu: “Vinh quang Đảng Cộng sản Việt Nam” [ 23/07/2020 00:00 ]
- Bài văn mẫu Nghị luận xã hội về tinh thần tự học Bài làm 1 [ 14/07/2020 00:00 ]
- Bài văn mẫu Nghị luận xã hội về tinh thần tự học Bài làm 2 [ 14/07/2020 00:00 ]
- Bài văn mẫu Nghị luận xã hội về tinh thần tự học Bài làm 3 [ 14/07/2020 00:00 ]
- Bài văn mẫu Nghị luận xã hội về tinh thần tự học Bài làm 4 [ 14/07/2020 00:00 ]
- Phương pháp làm bài tập điền vào bài đọc môn Anh [ 07/07/2019 00:00 ]
- Cách chọn từ điển phù hợp để học tiếng Anh hiệu quả [ 05/07/2019 22:05 ]
- 5 MẸO NÓI TIẾNG ANH LƯU LOÁT NHƯ NGƯỜI BẢN NGỮ [ 05/07/2019 21:22 ]
- Phương pháp học tiếng Anh hiệu quả [ 05/07/2019 21:16 ]
- HƯỚNG DẪN KỸ NĂNG ĐỌC SÁCH VÀ PHÁT TRIỂN VĂN HÓA ĐỌC CHO THIẾU NHI [ 05/07/2019 00:00 ]
- Các thể thơ thường gặp và cách đơn giản để nhận biết [ 04/07/2019 00:00 ]
- Tổng hợp dẫn chứng cho bài Nghị luận xã hội [ 04/07/2019 00:00 ]
- Khái quát các tác giả và tác phẩm trong chương trình thi THPT Quốc Gia môn văn [ 04/07/2019 00:00 ]
- Những dạng đề về Ai đã đặt tên cho dòng sông- Hoàng Phủ Ngọc Tường [ 04/07/2019 00:00 ]
- Kiến thức cơ bản và những đề thi liên quan đến bài Vợ chồng A Phủ Tô Hoài [ 04/07/2019 00:00 ]
Văn bản mới
- Quyết định về việc công nhận thí sinh trúng tuyển hệ liên thông từ trung cấp lên đại học ...
- Tuyển sinh liên thông từ TC lên ĐH ngành Khoa học Thư viện.
- Quyết định về việc công nhận thí sinh trúng tuyển hệ liên thông từ TC lên ĐH hình thức VLVH ...
- Quyết định về việc miễn học phí cho sinh viên Nguyễn Thị Lan lớp Khoa học Thư viện hệ VLVH ...
- Đăng ký học cùng lúc hai chương trình
- Tuyển sinh liên thông từ TC lên ĐH nghành Khoa học Thư viện.
- Tuyển sinh ngành Khoa học Thư viện.
- Quyết định về việc công nhận sinh viên tốt nghiệp ĐH hệ liên thông từ TC lên ĐH hình thức ...
- Ấn định tên đề tài và giảng viên hướng dẫn đề tài sinh viên nghiên cứu khoa học năm ...
- Tuyển sinh lớp bồi dưỡng nghiệp vụ về khoa học Thư viện (Chương trình Thư viện - Thiết bị ...
- Tuyển sinh liên thông từ TC lên ĐH ngành Khoa học Thư viện.
- danh sách lớp học phần K13
- V/v tổ chức Hội nghị CB,VC năm học 2015-2016.
- Tập huấn công tác Phòng cháy chữa cháy trong nhà trường
- Cử giáo viên tham gia công tác chủ nhiệm và cố vấn học tập năm học 2015-2016
Liên kết website
Thống kê website
Lượt truy câp: 3757896
Trong ngày:
Đang online: 12


